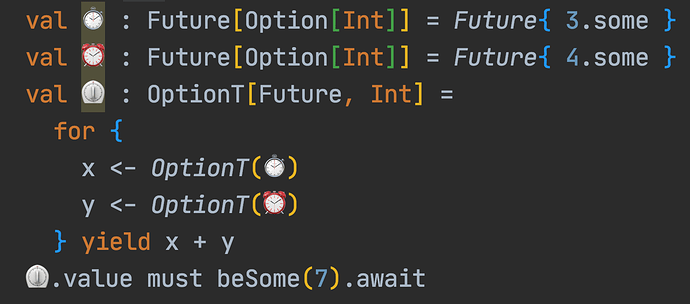
I mean, I get the map part, but what is flat? Flat in what sense?
Let’s start with map.
The map function has the following signature:
def map[F[_], A, B](fa: F[A])(f: A => B): F[B]
Which we can read like:
For a given effect F (also called contexts, or containers), if we have some effectual value fa (or type F of A, F[A]) and a function from A to B, A => B. It will return a new effectual value of type B, F[B].
So, the idea of the map function is to apply normal (also called plain) function to an effectual value.
In other words, the map function allows us to forget about managing the effect and just focus on the values. The function will take care of the unwrapping and wrapping that has to be done.
So a typical example would be the following.
We will use on the most basic effects, the Option (which represents the possibility of the absence of a value), to model a safe division.
def safeDivision(x: Int, y: Int): Option[Int] =
if (y != 0) Some(x / y) else None
Now, if we have to compute the following arithmetic expression: y = a + b / c
We could do something like this:
def foo(a: Int, b: Int, c: Int): Option[Int] =
safeDivision(b, c) match {
case Some(temp) => Some(temp + a)
case None => None
}
However, look at all that boilerplate; we have to manually unwrap and wrap again all the time.
A more complex expression would be a nightmare and we could easily make mistakes.
Enter map
def map[A, B](oa: Option[A])(f: A => B): Option[B] = oa match {
case Some(a) => Some(f(a))
case None => None
}
def foo(a: Int, b: Int, c: Int): Option[Int] =
map(safeDivision(b, c))(temp => temp + a)
Great!
Now, what happens if we want to compute this new expression: y = (a / b) / c
Well, we could try to do the same as before…
def bar(a: Int, b: Int, c: Int): Option[Option[Int]] =
map(safeDivision(a, b))(temp => safeDivision(temp, c))
Which we may say it works… but having to handle that nesting is not really nice.
And again a complex expression would result in a very nested structure.
Also, we actually do not care if the first division failed or the second, we just care that the complete expression failed.
So, it is time to meet another helper function, flatten.
def flatten[F[_], A](ffa: F[F[A]]): F[A]
Which again, reads as follows:
For a nested effectual value, return a no-nested effectual value. Which we may call that process a flattening over the value; we flatten the two Fs into one F.
Applying that to our previous function we get the following:
def flatten(ooa: Option[Option[A]]): Option[A] = ooa match {
case Some(Some(a)) => Some(a)
case Some(None) => None
case None => None
}
def bar(a: Int, b: Int, c: Int): Option[Int] =
flatten(map(safeDivision(a, b))(temp => safeDivision(temp, c)))
But, as you may have already guessed that process of mapping and then flattening is pretty common, so we may create a helper flatMap:
def flatMap[F[_], A, B](fa: F[A])(f: A => F[B]): F[B] =
flatten(map(fa)(f))
Which we can read as:
Given an effectual value and a function that returns a new effectual value, map the function and the flatten the result.
So we can again refactor our previous example as:
def bar(a: Int, b: Int, c: Int): Option[Int] =
flatMap(safeDivision(a, b))(temp => safeDivision(temp, c)))
// Or with normal method like syntax
safeDivision(a, b).flatMap(temp => safeDivision(temp, c))
// Or with for:
for {
temp <- safeDivision(a, b)
result <- safeDivision(temp, c)
} yield result
Hope this helps