Unexpected match type case matching

Question
1

I defined a simple type-level function to compute the sum of two nats. Oddly, in the match type, (_0, _1) seems to match the pattern (_, _0)…

Here is the code (or in Scastie):

sealed trait NatT
final case class Zero() extends NatT
final case class Succ[N <: NatT](n: N) extends NatT

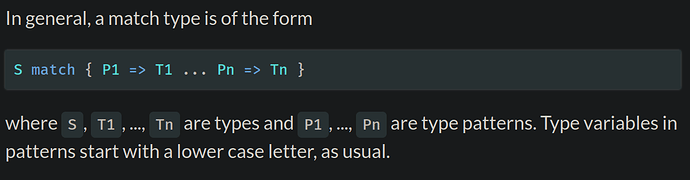
type Sum[X <: NatT, Y <: NatT] = (X, Y) match
  case (_, _0) => X
  case (_0, _) => Y
  case (Succ[x], Succ[y]) => Succ[Succ[Sum[x, y]]]

@main def main(): Unit =
  _1: Sum[_1, _0]
  _1: Sum[_0, _1]

type _0 = Zero
type _1 = Succ[_0]

val _0: _0 = Zero()
val _1: _1 = Succ(_0)

The expanded compiler error:

12 |  _1: Sum[_0, _1]
   |  ^^
   |  Found:    (_1 : _1)
   |  Required: Sum[_0, _1]
   |----------------------------------------------------------------------------
   | Explanation (enabled by `-explain`)
   |- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
   |
   | Tree: _1
   | I tried to show that
   |   (_1 : _1)
   | conforms to
   |   Sum[_0, _1]
   | but the comparison trace ended with `false`:
   |
   |   ==> (_1 : _1)  <:  Sum[_0, _1]
   |     ==> (_1 : _1)  <:  _0
   |       ==> (_1 : _1)  <:  Zero
   |         ==> _1  <:  Zero (left is approximated)
   |           ==> Succ[_0]  <:  Zero (left is approximated)
   |           <== Succ[_0]  <:  Zero (left is approximated) = false
   |         <== _1  <:  Zero (left is approximated) = false
   |       <== (_1 : _1)  <:  Zero = false
   |     <== (_1 : _1)  <:  _0 = false
   |   <== (_1 : _1)  <:  Sum[_0, _1] = false
   |
   | The tests were made under the empty constraint
    ----------------------------------------------------------------------------
2

it works if you change:

to: Scastie - An interactive playground for Scala.

  case (_, Zero) => X
  case (Zero, _) => Y

or: Scastie - An interactive playground for Scala.

  case (_, `_0`) => X
  case (`_0`, _) => Y
2 Likes
3

I see! So it seems that using type aliases is fine when they are the whole pattern, like case _0 => X, but not when they are a part of a larger pattern, like case (_, _0) => X.

I wonder whether there is some reasonable justification for this behavior.

4

I think it’s more likely that the compiler is confused by your use of underscores. You might want to read Chapter 6.10 of “Programming in Scala 5th Edition” which talks about identifiers in detail. It shows a few compiler errors due to underscore usage in identifiers. It also shows the use of backticked identifiers like @tarsa showed.

The rules for the type alias identifiers and cases in type patterns might be even more restrictive, not sure. Maybe it’s related to this?

Screenshot from 2022-08-05 11-49-32
Screenshot from 2022-08-05 11-49-321192×311 36.1 KB

5

I’d say that behaviour is against overall Scala’s regularity principles, i.e. my bet would be that Scala authors would prefer consistent behavior, but somehow some cases weren’t properly tested.

1 Like