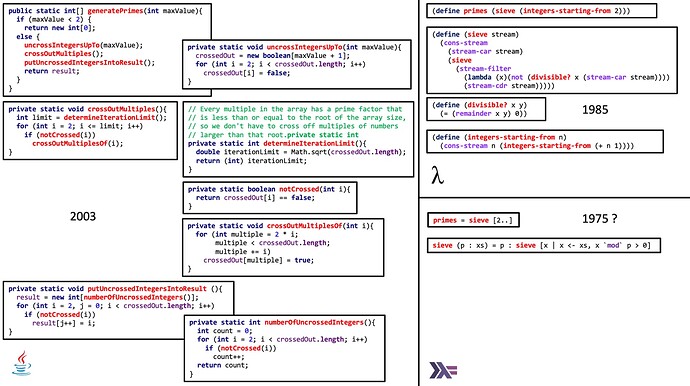
How the effort required to read an understand the Sieve of Eratosthenes varies greatly depending on the programming paradigm used to implement the algorithm.
2 Likes
Related reading: https://www.cs.hmc.edu/~oneill/papers/Sieve-JFP.pdf
And here is a gem from the good old days:
Algorithmically challenged: Sieve of Eratosthenes (the real one) Scala One-Liner
1 Like
@odd Very interesting - Thank you
1 Like
new slide deck: The Sieve of Eratosthenes - Part II - Genuine versus Unfaithful Sieve - thank you @odd for pointing me to the paper “The Genuine Sieve of Eratosthenes” - download for best viewing The Sieve of Eratosthenes - Part II - Genuine versus Unfaithful Sieve…
1 Like
I agree with the general sentiment, but for what it’s worth, the imperative example seems like a cherry-picked strawman. Here is a mutable scala implementation that is significantly more efficient, but still concise and a lot more understandable than the java sample:
def primesUntil(n: Int): collection.BitSet = {
val isPrime = collection.mutable.BitSet(n)
// optimize sieve by considering only odd numbers
(3 until n by 2).foreach(isPrime += _)
isPrime += 2
for
m <- 3 to sqrt(n).toInt by 2 if isPrime(m)
k <- m*3 until n by m*2
do isPrime -= k
isPrime
}
Modern java can look look a lot more like what I’ve written. How much less maintainable is this than the functional version? (could rename m to nextPrime and k to multiple for clarity)
3 Likes
Related post - Sieve of Eratosthenes: Finding All Prime Numbers - InterviewBit for finding all prime numbers with different approaches.
1 Like
Thank you @stewSquared.
One thing that fascinates me is the possibility that in the past (some) people might have spent decades in a one-paradigm bubble, in which they were only exposed to particular approaches
