As you may already know  I am fascinated by tessellations…
I am fascinated by tessellations…
I have now published, see Tessella - Regular polygon tessellation editor, a browser-based graphic editor for edge-to-edge regular polygon tessellations of the plane. It is built on Scala.js and Laminar and my own Tessella library.
I am really interested in any feedback or idea you may have on existing or future features.
6 Likes
Neat! How accurate are the “overlap” calculations?
Interesting new features might be:
- fit the largest possible polygon here
- recursively fill/color according to a pattern
Excellent question. Right now calculations use BigDecimal, with spire.math trigonometric functions. I experimented with spire’s Real but it is just too slow. And since calculations involve Pi, Algebraic is not going to work (assuming the performance gain was interesting enough, I do not know).
So the editor is relying on imprecise types and slowly accumulates a drift.
I tried to benchmark it, with n the number of steps and:
Double
Error for n=100: 4.176590108694379E-13
Error for n=1000: 1.381990763731864E-10
Error for n=10000: 4.1301551531602214E-9
Error for n=100000: 1.215472248992649E-5
BigDecimal
BigDecimal error for n=100: 7.591750418706819872570204290189428E-15
BigDecimal error for n=1000: 7.590514173330916840466619594168763E-14
BigDecimal error for n=10000: 7.590501812300311707232750901561907E-13
BigDecimal error for n=100000: 7.590501688660236113972658765823727E-12
I think it is acceptable, since I doubt that I will ever construct a finite tessellation with more than say one thousand polygons.
P.S. Please note that you can avoid the validation error you are showing, if you switch to Validation: OFF. In that case, the added polygon can touch or cross the perimeter edges.
Clear, and an acceptable approach in general. But, although this error is small, you don’t need to make 100000 steps to cause an issue. In the example below a partial hexagonal tessellation is shown which is known to be exactly area filling.
Now, your program refuses to place the hexagon here (if we do not override the error). Would it be possible to incorporate the accumulated error and compare it to the overlap? If the overlap is in the order of the error, it should not refuse or just warn. Or maybe it should display the log of the ratio. Then the user can decide if it’s a valid continuation.
Succes with this nice application!
Let me start saying that I love seeing how you are using the editor!
Regarding your point: your example to me it is saying that the editor is still working within the desired precision. Because:
-
After all the accumulated calculations it is still exactly pinpointing that the additional hexagon will have two vertices, not belonging to the shared side, that will touch the perimeter (boundary) of the finite tessellation
-
With Validation: ON this is invalid and the underlying reason is that the figure you are trying to create is no longer a finite tessellation of regular polygons. In fact you would create an external perimeter (boundary) and an internal one. But we cannot have an internal boundary, it is just an internal polygon, which is not regular (and of 19*6=114 sides, if I am counting correctly).
So the precision error here does not really matter and it not causing issues in your example. It is the logic of the editor to allow only strict finite tessellations of regular polygons, or not. And personally, since my research is more artistic than mathematical, I often use it without validation to allow the kind of “holes” you are also creating. But those holes are just (transparent) irregular (unit-sided) polygons, if we want to mathematically describe them.
I am attaching two images to better explain what I am saying.
The first is an editor output:
and the second is a painting:
2 Likes
I see. In the artistic mode its a lot of fun indeed: 
1 Like
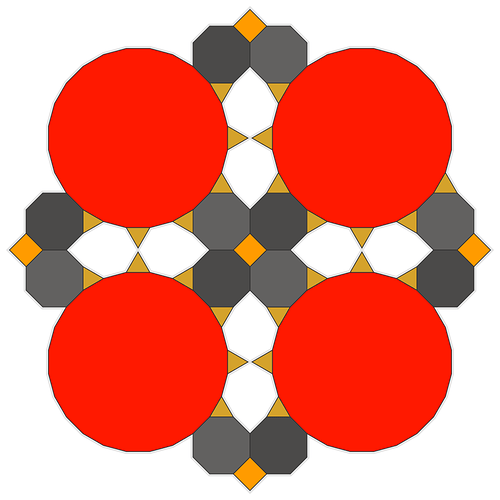
Nice one! I have many interesting designs involving the pentagon and a 5-fold radial symmetry. Just as an example:
1 Like
![]() I am fascinated by tessellations…
I am fascinated by tessellations…