how can we solve this special string Again problem using scala ,
https://www.hackerrank.com/challenges/special-palindrome-again/problem?h_l=interview&playlist_slugs%5B%5D=interview-preparation-kit&playlist_slugs%5B%5D=strings
What’s your idea for an approach to solving this, independent of “the Scala way”? What have you tried so far and where did you get stuck?
Here is the problem description for anyone who doesn’t feel like clicking:
A string is said to be a special string if either of two conditions is met:
- All of the characters are the same, e.g.
aaa.- All characters except the middle one are the same, e.g.
aadaa.A special substring is any substring of a string which meets one of those criteria. Given a string, determine how many special substrings can be formed from it.
Example
s=mnonopoo
scontains the following 12 special substrings:
{ m, n, o, n , o, p, o, o, non, ono, opo, oo }
So it seems like:
- Every letter of the string is considered a “special substring”, even if they aren’t unique
- You need to do a “sliding window” walk from one end to the next, gradually increasing character length of the window and “offset” of the window.
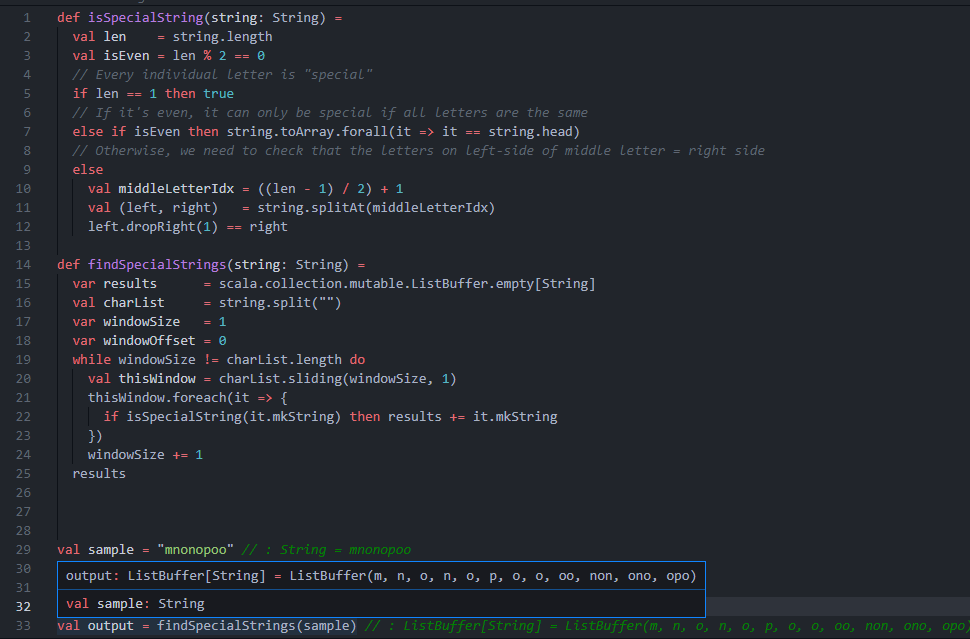
def isSpecialString(string: String) =
val len = string.length
val isEven = len % 2 == 0
// Every individual letter is "special"
if len == 1 then true
// If it's even, it can only be special if all letters are the same
else if isEven then string.toArray.forall(it => it == string.head)
// Otherwise, we need to check that the letters on left-side of middle letter = right side
else
val middleLetterIdx = ((len - 1) / 2) + 1
val (left, right) = string.splitAt(middleLetterIdx)
left.dropRight(1) == right
def findSpecialStrings(string: String) =
var results = scala.collection.mutable.Seq.empty[String]
val charList = string.split("")
var windowSize = 1
var windowOffset = 0
while windowSize != charList.length do
val thisWindow = charList.sliding(windowSize, 1)
thisWindow.foreach(it => {
if isSpecialString(it.mkString) then results +: it.mkString
})
windowSize += 1
results
val sample = "mnonopoo"
findSpecialStrings(sample)
So to traverse mnonopoo, it would look like this:
Results = []
"Window size" = 1
"Window offset" = 0
------------------------
[Offset]
(empty)
m n o n o p o o
^
[Window]
------------------------
Outcome: Add to results = `m`
Results = [m]
"Window size" = 1
"Window offset" = 1
------------------------
[Offset]
v
m n o n o p o o
^
[Window]
------------------------
Outcome: Add to results = `n`
This continues from (Window Offset = 0 .. string.length - 1)
At this point, our results contain all individual letters of the string itself
Let’s skip forward, to starting the walk with Window Size = 2
Results = [m, n, o, n , o, p, o, o]
"Window size" = 2
"Window offset" = 0
------------------------
[Offset]
(empty)
m n o n o p o o
^ ^
[Window]
------------------------
Outcome: `mn` is not a "Special string", skip
Again skipping forward until the next match is found:
Results = [m, n, o, n , o, p, o, o]
"Window size" = 2
"Window offset" = 6
------------------------
[Offset]
v
m n o n o p o o
^ ^
[Window]
------------------------
Outcome: Add to results = `oo`
And now skipping until Window size = 3
Results = [m, n, o, n , o, p, o, o, oo]
"Window size" = 3
"Window offset" = 0
------------------------
[Offset]
(empty)
m n o n o p o o
^ ^ ^
[Window]
------------------------
Outcome: `mno` is not a "Special string", skip
On next iteration, another match is found
Results = [m, n, o, n , o, p, o, o, oo]
"Window size" = 3
"Window offset" = 1
------------------------
[Offset]
v
m n o n o p o o
^ ^ ^
[Window]
------------------------
Outcome: Add to results = `non`
Results = [m, n, o, n , o, p, o, o, oo, non]
"Window size" = 3
"Window offset" = 2
------------------------
[Offset]
v
m n o n o p o o
^ ^ ^
[Window]
------------------------
Outcome: Add to results = `ono`
First, I’d be reluctant to provide a full solution to a homework question that doesn’t contain any evidence that the poster has taken a stab at the problem at all…
AFAICS there’s at least two problems with the code as posted - an off-by-one and a wrong operator. To my taste, mutable collections and while loops don’t really represent “the Scala way”, but that’s a subjective judgement.
This seems to come with a complexity of # window sizes × # windows (i.e. n / window size) × isSpecialString predicate (~ linear in window size), i.e. in the ballpark of O(n³), n being the length of the input. Note that the problem statement requires only the result count, for input sizes up to 1M. This approach may not scale up to the bigger inputs in this range, there should be a more computationally efficient solution.
First, I’d be reluctant to provide a full solution to a homework question that doesn’t contain any evidence that the poster has taken a stab at the problem at all…
The solutions can be found in the comments or by googling the problem name. For Scala, you can either take an existing one or run any Java solution through Intellij’s “Java → Scala” converter.
Seems like a lot of effort for potentially no payoff ![]()
AFAICS there’s at least two problems with the code as posted - an off-by-one and a wrong operator. To my taste, mutable collections and while loops don’t really represent “the Scala way”, but that’s a subjective judgement.
This approach may not scale up to the bigger inputs in this range, there should be a more computationally efficient solution.
There’s no off-by-one error, run the solution in Scastie:
I had no idea what operator to use for mutable collections though, I’ve never used them before.
It looks like I wanted ListBuffer and +=
Also the foreach would probably have been better written as:
thisWindow.filter(it => isSpecialString(it.mkString)).foreach(it => results += it.mkString)
Would be interested in seeing better solutions, which I garner was the point of this post, and I’m the only one who has posted so far =/
Alternatively:
def findSpecialStrings(string: String) =
val charList = string.split("")
(1 to charList.length)
.flatMap(window => charList.sliding(window, 1).map(_.mkString).filter(isSpecialString))
Sure, but this requires some basic understanding of problem, solution and implementation language, and at least a bit of effort. ![]() (And it’s not that likely to come up with quality code.)
(And it’s not that likely to come up with quality code.)
Try “aaaa” (sample input 2 in the problem description), or just “a”.
Because some people shy away from doing other’s homework…? ![]()
Anyway, since you mentioned the comments, I’ve now seen there’s a Python(?) solution that uses a similar approach to what I’ve come up with: Transform to RLE, use arithmetic series sum for the first case and sliding window of 3 with min for the second. Unless I’m missing something, this should be in O(n) overall. Perhaps I’ll post my take here in a few days’ time.
…just realized there’s another issue: Check “abcab”.
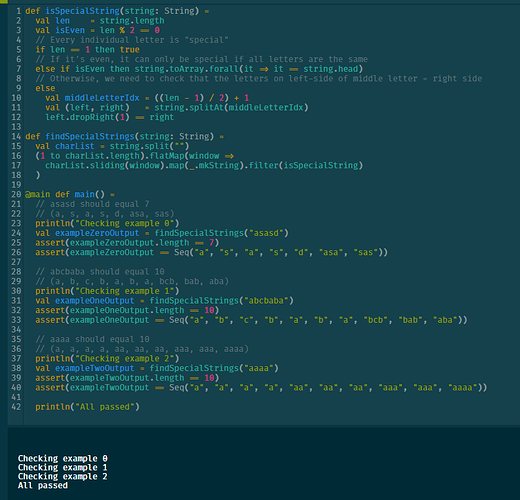
Using the second one posted above, "Alternatively: <flatMap/sliding/map/filter impl>"
def findSpecialStrings(string: String) =
val charList = string.split("")
(1 to charList.length).flatMap(window =>
charList.sliding(window).map(_.mkString).filter(isSpecialString)
)
All examples pass 
“a”/“aaaa” works with this change; the off-by-one was in the while condition. “abcab” still is classified as special.
Almost a week should hopefully be enough time for any homework deadline to have passed.  (As expected, the OP didn’t seem too interested in a discussion.) Here’s my take:
(As expected, the OP didn’t seem too interested in a discussion.) Here’s my take:
/** positive int > 0 */
type Nat = Int
/** non-negative int >= 0 */
type Nat0 = Int
/** run-length encoded list: [a,a,b,c,c,c] ~ [(a,2),(b,1),(c,3)] */
type RLE[T] = List[(T, Nat)]
object RLE:
def apply[T](es: IterableOnce[T]): RLE[T] =
es.iterator.foldLeft[RLE[T]](Nil) {
case ((prev, cnt) :: t, cur) if prev == cur =>
prev -> (cnt + 1) :: t
case (res, cur) => cur -> 1 :: res
}.reverse
/** arithmetic series sum: 1 + ... + n */
def sumSeries(n: Nat): Nat = n * (n + 1) / 2
/** ex.: ...,(a,3),... -> |[aaa,aa,aa,a,a,a]| = 1+2+3 */
private def caseOneCount(rle: RLE[Char]): Nat0 =
rle.foldLeft(0) { (acc, cur) => acc + sumSeries(cur(1)) }
/** ex.: ...,(a,3),(b,1),(a,2),... -> |[aba,aabaa]| = min(3,2) */
private def caseTwoCount(rle: RLE[Char]): Nat0 =
rle
.sliding(3)
.foldLeft(0) {
case (cnt, List((lch, lcnt), (mch, 1), (rch, rcnt))) if lch == rch && mch != lch =>
cnt + (lcnt min rcnt)
case (cnt, _) => cnt
}
/**
* total count of "special" substrings in the given string,
* see https://www.hackerrank.com/challenges/special-palindrome-again/problem
*/
def specialCount(s: String): Nat0 =
val rle = RLE(s)
caseOneCount(rle) + caseTwoCount(rle)
This isn’t as performant as it could be, of course, but I think it should be sufficient for the scope of the exercise, and I’d hope it expresses the implementation idea quite clearly. (I also couldn’t find any library-level microbenchmarking tool that supports Scala 3 and didn’t want to go through the contortions of creating a JMH setup, and hunting performance without decent measurements is futile.)
Any pointers to flaws or improvement suggestions are welcome, of course!
As an aside, I’ve been wondering what a Scalacheck test might look for this, and I ran into the same problem as usual when trying to apply outside formal/abstract, naturally “law-based” domains: Either the tests only cover some classes of special cases, or I end up reinventing the actual algorithm in the test. 
The best I could come up with is this little gem:
val alphabet: String = "abcd"
def inpListGen(chars: String): Gen[List[Char]] =
Gen.listOf(Gen.oneOf(chars))
test("specialCount: append") {
forAll(inpListGen(alphabet), Gen.oneOf(alphabet)) { (cs, c) =>
def case2SingleRhsContrib(y: Char, zc: Nat) =
if(y == c && zc == 1) 1 else 0
def case2AddedRhsContrib(x: Char, y: Char, xc: Nat, yc: Nat, zc: Nat) =
if(x == c && y != c && yc == 1 && xc > zc) 1 else 0
val contrib =
RLE(cs).takeRight(3) match {
case List((`c`, zc)) => zc
case List((y, yc), (z, zc)) =>
if(z == c) zc else case2SingleRhsContrib(y, zc)
case List((x, xc), (y, yc), (z, zc)) =>
if z == c
then zc + case2AddedRhsContrib(x, y, xc, yc, zc)
else case2SingleRhsContrib(y, zc)
case _ => 0
}
val s = cs.mkString
specialCount(s :+ c) should be (specialCount(s) + 1 + contrib)
}
}
This inductively asserts the increase of the “special count” when a single char is added. It feels more complicated than the actual implementation, and this could be turned into an alternative implementation where the RLE representation is kept as internal state and built iteratively as each successive char is considered - IOW, it’s at least pretty close to reinventing the actual algorithm…
Any suggestions for improvement are appreciated.
Looks pretty similar to what I’ve come up with.
I think you could drop the reverse call as it doesn’t matter whether you read the string from left to right or in the other direction.
Also, you could simplifiy the condition in the case guard to:
case (cnt, List((lch, lcnt), (_, 1), (rch, rcnt))) if lch == rch =>
since you already ensured that the next character is always different from the preceding one by the RLE.
Bonus points for the take on the scalacheck spec. I haven’t really thought about this yet… 
Right, but I wanted to keep the LRE part such that it could theoretically be pulled in from the outside and/or could be used for other purposes that require the original order.
Of course. ![]() Thanks!
Thanks!
hey all,
thanks for the posts.
it was not homework, I was just trying out some problems online and learn scala bit by bit.
my solution was very bad and time issues arises so wanted to know a better one also if scala has a better way of solving it.
// Complete the substrCount function below.
def substrCount(n: Int, s: String): Long = {
var result =s.size
val arr= s.toCharArray
var myList = List[String]()
def isValid(m:String):Unit ={
var setval=m.split("").toSet
if (setval.size <=2){
var v_strArr=m.toCharArray
if(v_strArr(0)==v_strArr(v_strArr.size-1) && (m.size%2) !=0 && setval.size>1)
myList :+= m
if(setval.size==1)
myList :+= m
}
}
for(x<-0 until n){
for(y<- x+1 until n){
if(arr(x)==arr(y))
{
isValid(s.substring(x,y+1)) }
}
}
println(myList)
result +=myList.size
println(result)
result
}
def main(args: Array[String]) {
val stdin = scala.io.StdIn
val printWriter = new PrintWriter(sys.env("OUTPUT_PATH"))
val n = stdin.readLine.trim.toInt
val s = stdin.readLine
val result = substrCount(n, s)
printWriter.println(result)
printWriter.close()
}
Then why not just state this and add your code to get the discussion started? There should be absolutely no harm in showing a “bad” solution - trying to improve is always a good thing. This way others will have a chance to pick up exactly where you are at right now and give advice related to your actual code. If you just throw a challenge without any indication that you worked on the problem and its solution yourself, you’re bound to encounter reactions just like mine - probably somebody just wants to have their homework done for them…
Here’s what I’d think is one possible, more “scalaesque” and readable reinterpretation of your code - opinions may differ, though:
def substrCount(n: Int, s: String): Long =
def contrib(startIdx: Int, endIdx: Int): Int =
if s.charAt(startIdx) == s.charAt(endIdx)
then
val ss = s.substring(startIdx, endIdx + 1)
ss.toSet.size match {
case 1 => 1
case 2 if ss.size % 2 != 0 => 1
case _ => 0
}
else
0
val ranges =
for {
startIdx <- (0 until s.length).iterator
endIdx <- ((startIdx + 1) until s.length).iterator
} yield (startIdx -> endIdx)
ranges.foldLeft(s.length) {
case (acc, (startIdx, endIdx)) =>
acc + contrib(startIdx, endIdx)
}
In particular I’ve done away with the array conversions and transformed the mutable state plus loop into a fold. In addition I have changed variable names and simplified a few other things. This should also be somewhat faster, too, but see below. (The “n” input param could be dropped, as well, that’s just for the poor C folks…) This is just a quick suggestion, and I’m pretty sure others could come up with further improvements.
The “specialness” check still is too lenient, though. Try “aaabaaa” as input - “abaaa” and “aaaba” will be accepted as “special” substrings.
Algorithmically, your approach seems pretty similar to the one @GavinRay has suggested: Generate all possible substrings and check them for “specialness”. (The main conceptual difference is that in your approach the “outer loop” goes over the substring start index, while in the other one it’s over substring length.) In both cases this amounts to O(n³) - the “innermost loop” in your case is hidden in the conversion to a set. This is bound to become computationally prohibitive pretty quickly for bigger inputs and cannot really be fixed by tweaking the code at the lower level. See my suggestion above for a different approach.
Here’s my approach. I didn’t run it in Hackerank so I don’t know it passes everything but it does pass the sample inputs.
Ideas behind this:
- Everything relates to a subsequence of the input, so no need to allocate a bunch of intermediate data structures and substrings, just move a cursor through the input
- The first type of special string is a contributor to the second type, so you can use the results of that calculation while determining the contribution of the second and basically do both at the same time
- Once a run of characters is accounted for as the first type of special string, it doesn’t need to be visited again, so the cursor only advances and makes this roughly
O(n) - Scala is multi-paradigm, so “the Scala way” depends heavily on the author, and I embrace the form that allows limited local mutability and doesn’t require everything use functional combinators
def substrCount(n: Int, s: String): Long = {
val end = n
def count(start: Int, expect: Char): Int = {
var c = 0
var idx = start
while(idx < end && s.charAt(idx) == expect) { c += 1; idx += 1 }
c
}
def sumSeries(i: Int): Long = (i * (i + 1)) >> 1
@scala.annotation.tailrec
def specials(prefixStart: Int, total: Long): Long = {
if (prefixStart < end) {
val c = s.charAt(prefixStart)
val prefixLen = count(prefixStart, c)
val prefixEnd = prefixStart + prefixLen
val suffixStart = prefixEnd + 1
val suffixLen = count(suffixStart, c)
val contrib = sumSeries(prefixLen) + prefixLen.min(suffixLen)
specials(prefixEnd, total + contrib)
} else {
total
}
}
specials(0, 0L)
}
It should be plenty quick even on the large inputs, and can be made quicker still since some portions of the input are visited an extra time or two unnecessarily. Essentially, the “suffix” part of a type-2 special string is itself a type-1 special string, and might be the start of its own type-2 special string. Accounting for this incrementally was starting to make the implementation feel complicated and I opted for simplicity. But it should be possible and if you can do it then it’d be nearly as fast as Scala would get since without the extra data structures and each character visited only once in order it would be quite cpu- and memory-friendly.
Passes my Scalacheck spec, as well.
Yup, as I said before, that’s a pretty subjective judgement, and it depends a lot on the purpose of the code - e.g. core library internals vs application level glue code.
If performance is not a pressing concern, I’d still prefer something along the lines of my implementation, as I find it easier to grasp the idea from reading the code. (Again, subjective.) If performance is important, though, your approach is clearly preferable. From an unreliable ad hoc micro benchmark (first number is result, second milliseconds):
1000
(jgu,(1028,0))
(pro,(1028,3))
10000
(jgu,(10377,1))
(pro,(10377,20))
100000
(jgu,(103802,3))
(pro,(103802,48))
1000000
(jgu,(1038693,6))
(pro,(1038693,428))
Nice! Thanks for doing that and the benchmark!
Yeah, yours is nice and a lot more explicit about the concepts it’s using/representing, for sure. It’s actually what inspired mine! If you squint, mine is almost your RLE approach after a fair bit of inlining and some leveraging of things that happen to work out for this task (like that you can always do the min because it’ll be 0 in the cases you don’t want it to contribute). Certainly it could use some explanatory comments, and I’d add them if it were anything other than a throwaway for a site to which I forgot I was even a member ![]()
Since we’re getting into solutions, this is a pretty compact way to actually literally generate all the strings:
def fragment(s: String, parts: List[String] = Nil): List[String] =
if (s.isEmpty) parts
else s.span(_ == s.head) match { case (l, r) => fragment(r, l :: parts) }
def simple(ss: List[String]): List[String] =
ss.flatMap(_.tails.filter(_.nonEmpty).zipWithIndex.flatMap{
case (s, n) => List.fill(n+1)(s)
})
def symmetric(a: String, b: String): List[String] =
a.tails.filter(_.nonEmpty).map(x => x + b + x).toList
def complex(ss: List[String], parts: List[String] = Nil): List[String] =
ss match {
case a :: b :: c :: more if b.length == 1 && a.head == c.head =>
complex(b :: c :: more, symmetric(a.take(c.length), b) ::: parts)
case a :: more => complex(more, parts)
case _ => parts
}
def solution(s: String): List[String] = fragment(s) match {
case parts => simple(parts).reverse ::: complex(parts)
}
If you only need counts, not strings, you can change it as follows:
def fragment(s: String, parts: List[String] = Nil): List[String] =
if (s.isEmpty) parts
else s.span(_ == s.head) match { case (l, r) => fragment(r, l :: parts) }
def simple(ss: List[String]): Int = ss.map(s => s.length*(s.length+1)/2).sum
def complex(ss: List[String], count: Int = 0): Int =
ss match {
case a :: b :: c :: more if b.length == 1 && a.head == c.head =>
complex(b :: c :: more, (a.length min c.length) + count)
case a :: more => complex(more, count)
case _ => count
}
def solution(s: String): Int = fragment(s) match {
case parts => simple(parts) + complex(parts)
}
There are various ways to optimize more, but basically a lot of these questions are solved by recursion, so either you find your own recursive solution, or use library functions to do it for you.