I have three different questions about how to best implement a particular algorithm in Scala. I’ve implemented the Bellman-Ford single source shortest path algorithm within a Graph class. Below is the code for the bellmanFord method, but I think most of the Graph implementation is unimportant for this question, except that the type variable A is the vertex type. (maybe V is a better type variable for this purpose?)
case class Graph[A](Vertices: Set[A], Edges: Set[Edge[A]]) {
...
}
The Bellman-Ford algorithm takes a graph and a source vertex and returns two values, 1) an mapping which given any vertex, v, gives the distance from the source to v. 2) a so-called precedence map which for any vertex, v, gives the preceding vertex along the shortest path from source to v. Using the precedence map, we can trace from anywhere back to the source.
A several questions about improving my implementation.
-
bellmanFordtakes aweightfunction which maps each graph edge to a weight. I’ve implemented the edge weight as an integer, but I’d really like it to be more general. Can I replaceEdge[A] => IntandMap[A,Int]with something more general to allow the return values of theweightfunction to be anything which supports+and<? -
The return value of
bellmanFordis of type(Map[A, Int], Map[A, A]). I have to reuse this type several times within the algorithm on the local functionsrelaxandrelaxationPass. I’ve defined a type aliasDPto reduce typing, but I suspect there’s a clearer way to do this. However, if I manage to encapsulate this ugly type into something more manageable, I need to make sure theIntinMap[A,Int]still is the same type as theIntin the previousEdge[A] => Int.
This somewhat complicated return type is avoided in mutating implementations such as in Python, because the bellmanFord function accepts two hash tables which it destructively modifies. I’d like to avoid these mutable objects.
- the local function
relaxationPassis a tail recursive function whose goal is to reduce the givendpseveral times,i-1times to be exact. Can’t I rewrite this somehow as call to some variant of fold/reduce which ignores its iteration variable?
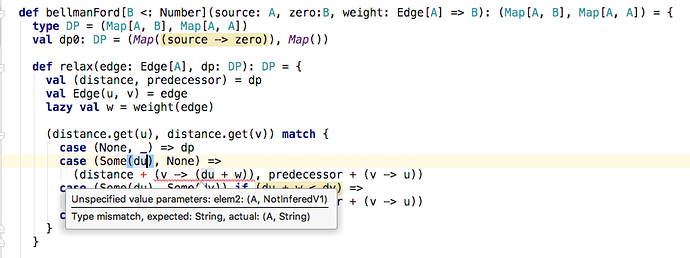
def bellmanFord(source: A, weight: Edge[A] => Int): (Map[A, Int], Map[A, A]) = {
type DP = (Map[A, Int], Map[A, A])
def relax(edge: Edge[A], dp: DP): DP = {
val (distance, predecessor) = dp
val Edge(u, v) = edge
lazy val w = weight(edge)
(distance.get(u), distance.get(v)) match {
case (None, _) => dp
case (Some(du), None) =>
(distance + (v -> (du + w)), predecessor + (v -> u))
case (Some(du), Some(dv)) if (du + w < dv) =>
(distance + (v -> (du + w)), predecessor + (v -> u))
case _ => dp
}
}
def relaxationPass(i: Int, dp: DP): DP = {
if (i == 0)
dp
else
relaxationPass(i - 1, edges.foldLeft(dp) {
(dp: DP, edge: Edge[A]) => relax(edge, dp)
})
}
relaxationPass(Vertices.size, (Map((source -> 0)), Map()))
}