I’ve seen several presentations in yesteryear about how to represent abstract algebra in Scala. For example: how to represent a monoid, group, ring, semiring, field, etc.
Can anyone recommend a good treatment/development of this?
I’m sure that Scala is able to model some things well, and some things less well.
I’ve been thinking about it and I don’t yet see any clean way to do it using the inheritance model of Scala. For example if I have an algorithm which should work for any monoid (such as fast exponentiation below), then algebraically speaking, since a group is a monoid, then the fast-exponentiation function should also work given a group. And ideally I should be able to pass the additive group of integers, or the finite multiplicative group of integers modulo 13.
def fastExponentiate[T](x:T, n:Int, monoid[T]):T = {
if (n == 0)
monoid.identity
else if (n == 1)
x
else if ( odd?(n))
monoid.op(x,fastExponentiate(x, n-1, monoid))
else { // even
val a = fastExponentiate(x, n/2, monoid)
monoid.op(a, a)
}
}
Another problem/challenge/modeling-question I see is that many of the algebraic structures obey many is-a relationships.
monoid-wikipedia
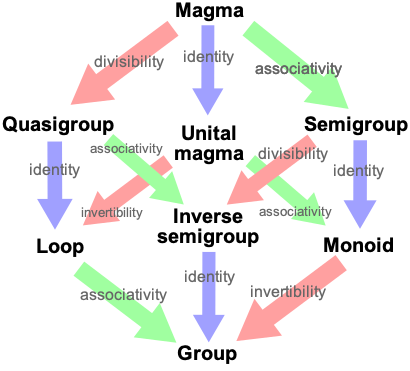
One would like to implement these relationship using OO inheritance, so that for example if a function needs a quasigroup, I could happily pass it an inverse semigroup, a loop, or a group.
On the other hand in algebra we say that a ring and a semi-ring is a group. But that’s not really the case. A ring (somehow) contains an additive group, and a multiplicative monoid. On the other hand a field IS a commutative ring, but (somehow) has/contains a multiplicative group made up of all its non-zero element with zero coming from the additive group of the commutative ring.
I’m pretty sure someone coming from Haskell would insist that OO inheritance is not the correct model. But then again he would argue that many common OO problems should be solved without inheritance. Since I don’t know Haskell, I would not be able to understand nor dispute such an argument.
I looked at one treatment, Monoids and Semigroups in Scala the author approaches the problem very different than I would. For example, at the end he demonstrates how to implement an object which contains a mapReduce function.
It is not clear to me how this generalizes in a way which lets me pass a group to the fastExponentiation function. Or how to write a matrix multiply function (which needs a semi-ring for + and *) in a way that I could also call matrix-multiply with a field which is-a semi-ring.
The motivating case where I wanted to use this was I’d like students to write property based tests to detect whether a given x which claims to be a (monoid, group,ring, field) actually obeys the axioms of that algebraic structure. For example if I generate 3 objects, does the associative rule apply? Does multiplying an element on the left and right by the identity return the element. Does every element have an inverse which can be multiplied on either left or right to return the identity?
Ideally I’d like to not implement the same check for monoid and group. Checking a group should implicitly check its monoid-ness. This makes me think that validation code belongs in the class itself rather than in the test case code. Or is it better to set up some sort of visitor pattern to allow the tests to inherit property-based-tests according to the hierarchy of the code being tested?
And then the student could ask the question: If I construct addition and multiplication of polynomials using rational coefficients and integer modulo 7 exponents, is that a ring? Is it a multiplicative group? etc. Or given two groups, is the Cartesian product with pair-wise addition also a group?
The “red book” covers some of this over several chapters with an approach using traits and “extends” Functional Programming in Scala
Alternatively you might want to look into type class derivation using “derives”, which is a very Haskell-like way Type Class Derivation | Scala 3 Language Reference | Scala Documentation
Finally there is this https://github.com/twitter/algebird They have Semigroup, Group, Monoid, Ring, Metric.
I’m sure there is more stuff out there. Found a really nice article here Adventures in Abstract Algebra Part I: Implementing Algebraic Structures in Scala · An Abstract Plane
Here is a nice intro, but his strategy is problematic when try to accommodate Ring and Field.
For example in the Scala object model. Group[Int](1,*) IS-A Monoid[Int](1,*). However Ring will not analogously work in the Scala model. Why? Because Ring(0,+,1*) needs to be both IS-A Group[Int](0,+) and simultaneously IS-A Monoid[Int](1,*). A Scala class cannot inherit the same trait twice in two different ways. If Ring extends Monoid and also Group which itself extends Monoid, there is ONLY ONE op method, and only one identity instance variable.
also from the point of view of Monoid the programmer would like to talk about op as the operation. However, from the point of view of Ring the programmer would like to talk about + and *. The Scala model (as I understand it) does not let different classes use different names to refer to the same instance variable.
There are of course ways to workaround this. For example by composition, but then that breaks IS-A relationships, and forces the subclasses to implement ad-hoc delegation. Not the end of the world of course.
Nevertheless, it is good to see this particular approach, and to contemplate how to improve it.
interesting implementation indeed. Thanks for the link.
BTW, what does @specialized mean? Does it mean that I can use any method on an object to type T which is common to Int, Long, Float, and Double ?
trait Ring[@specialized(Int, Long, Float, Double) T] extends Group[T] with CommutativeGroup[T] with ARing[T] {
override def one: T
override def times(a: T, b: T): T
override def product(iter: TraversableOnce[T]): T =
if (iter.isEmpty) one // avoid hitting one as some have abused Ring for Rng
else iter.reduce(times)
}
Interesting that in both those implementation, Ring is-a additive Group, but not a multiplicative Monoid. It is an interesting, but unsatisfying design choice.
it is also very interesting in this implementation that the author makes finite monoids, groups etc be extensions of more general algebraic structures by creating a trait for finiteAlgebraicStructure. That’s clever.
Have you looked at Spire yet? That has usually been my go-to for such things. As usual, it doesn’t do it with inheritance (which doesn’t really work, for the reasons you point out), but with type classes. (Type classes are almost always the answer for complex problems like this.)
No I haven’t looked at it, at least in a long time. I think I may have seen it loooong ago for a very different reason.
No, @specialized is an optimization, it will generate separate classes that use the listed types (which have to be value types) directly instead of generically, so they don’t require boxing (if you’re familiar with Java, it’s similar to how Java has separate Stream and IntStream classes for performance reasons, but without having separate classes from the user perspective and without duplicate implementations). The tradeoff is of course, that generating the specialized classes increases the size of the compiled program.
(PS: I tried to look up the documentation, but couldn’t find it. Is there any official documentation of the feature aside from the annotation’s vague scaladoc?)
see SID-9 - Scala Specialization | Scala Documentation (the actual PDF is two clicks further down, but I’m posting this URL as likely the most stable URL)
It seems that experts disagree. The discussion in another thread is that typeclasses fail to solve this issue other thread inasmuch as certain aspects cannot be determined at compile time, and the compiler cannot determine in many cases which evidence object to use.
What I did there was implement something based on typeclasses, but which experts pointed out does not fix the definition of a typeclass.
I think that’s a bit of overstatement. Monoids are specifically controversial, because of the fact that there are multiple valid instances in many situations.
That said, I’ve always done Monoids with type classes anyway, and it’s hugely convenient. You just make sure that you have the correct instance in scope, which is rarely complicated. When it is not obvious, you just pass the instance by hand instead of implicitly. (There is nothing stopping you from providing them manually when necessary – it’s just not the way you usually do it, because it is excess boilerplate in most cases.)
And to be clear: what you showed there was not a normal type class – type classes are almost always implemented in terms of a second parameter list, with the type class provided implicitly.
Hi Jim, I have developed some algebraic structures in Scala. They start with simple structures like semigroup or abelian group but it continues with rings, fields, quadratic fields, polynomial, etc… and even quaternion algebras. You can take a look at them in:
https://github.com/zplot/algebra9/tree/main/src
Please, be aware that all this code is just an exercise and it does not pretend more than learning algebra by coding scala and learning scala by practicing algebra.
I hope it can give you some ideas.