I’m a Scalar beginner and ran into this "0.1 * 0.1=0.010000000000000002 "

.
Can someone tell me how I should understand this behavior?
Thank you.
It’s called floating point arithmetic
Here’s an idea. I’m sure it’s not original, and it may cause bigger problems than it solves, but I’ll “float” it for feedback.
Why not put some basic cleanup rules in the print function for floating-point numbers? After the number is converted to a string, check the mantissa for, say, 14 or more consecutive zeros followed by a digit. If that pattern is found, just lop off the zeros and the digit for the printout. Similarly, if 14 or more nines are found, lop them off and increment the preceding digit by one.
Has anything like that ever actually been done in a major language standard?
But how would you distinguish from a number that has this pattern but is correct?
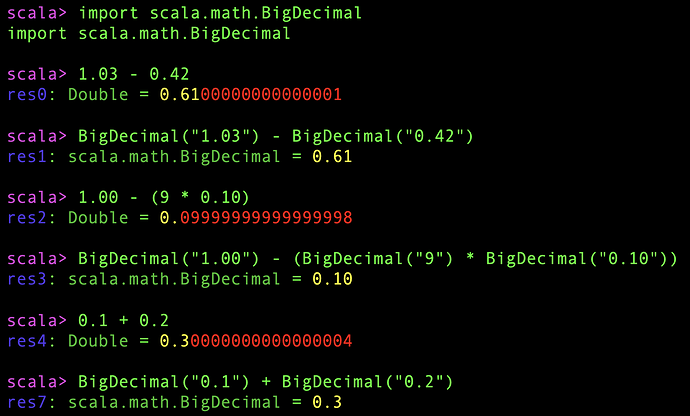
The solution to this is to use BigDecimal when you need the precision (let’s say you are working with money) and you can sacrifice the performance.
If they called it “breaking point arithmetic”, people might be less confused. Or at least harbor lowered expectations.
But how would you distinguish from a number that has this pattern but is correct?
Can you provide an example outside of pure mathematics where that could happen?
If you have a string of 14 zeros or 14 nines in a floating-point number, I can’t imagine any practical application where you would lose any significant information by simply eliminating them for printed output.
The closest example that I can come up with is unix time (time in seconds since New Years 1970), but even there It is hard to come up with a situation where the pattern could represent real information. Using standard 64-bit arithmetic, you can get down to a few microseconds of precision.
As for money, is it actually continuous or discrete? Is the penny indivisible? I suspect derivative traders would say yes. And so would gas station owners, whose price per gallon always ends with .9 cents! So if money is actually continuous, it seems to me that using BigDecimal is no more “correct” than just rounding or truncating the output to whatever level of precision is deemed appropriate.
Why? This would just be sweeping a problem under the rug that developers need to be aware of, anyway, even if they don’t care about this level of precision.
For example, this would feel way more confusing to me than the explicit floating error:
scala> 0.1 * 0.1
val res0: Double = 0.01
scala> res0 == 0.01
val res1: Boolean = false
With the proposed rule, you couldn’t distinguish exact values (1.0 / 2 == 0.5) from inexact ones (0.1 * 0.1 ~ 0.01). And if you are actually accumulating errors, this would start showing up out of nowhere at some rather arbitrary point instead of being traceable from the beginning, e.g.
scala> Iterator.iterate(0.0)(_ + 0.1 * 0.1).drop(15).take(2).toList
val res0: List[String] = List(0.15, 0.1600000000000001)
I’d rather think it’s beneficial to have this issue exposed in generic developer facing output. As for user facing output, you control it. You can either simply dial down precision (e.g. f"${0.1 * 0.1}%.16f"), or even implement your rule, if it suits your user base.
I agree that the basic cleanup rules I proposed should not be hard-wired into the language itself. What I was proposing makes sense for a calculator, however. We all know that 0.1 * 0.1 = 0.01, not 0.010000000000000002. If someone wants to use the REPL as a calculator, I doubt they want to see those tiny numerical errors. So maybe there should be a special REPL calculator mode that applies the rules I suggested.
As for the example you provided showing how my cleanup rules might confuse the user, I don’t see how that is any more confusing than what happens already:
scala> 0.1 * 0.1 == 0.01
val res0: Boolean = false
I mean, this concept exists in some test frameworks – it’s not unusual to define a concept of an epsilon for equality matching in tests. (It’s been a while, but I’m fairly sure ScalaTest has this.) It makes sense there, enabling the user to explicitly say that they are looking for inexact equality, and giving them sufficient control over what that means. But I doubt I would want that in the REPL, personally.
Defining an epsilon for equality testing is not quite the same as what we are talking about here, although the objective is similar. I just find it interesting that by converting a binary number to a decimal string it is possible, with very basic pattern matching, to correct certain numerical errors due to floating-point arithmetic. And I wonder how far the concept can be taken. That’s all.
Perhaps, but perhaps BigDecimal would be a better choice there, anyway. But even if you’re using double, that’s user facing output - you can shape it any way you want. This discussion strand, as I understand it, is about the default representation mostly used for developer facing output. (Actually it might help to have explicit, separate concepts for those two, such as Debug and Display in Rust. EDIT: If you are using cats, anyway, you might opt to use Show for the latter by convention.)
Here I at least have a chance to investigate further. I can check the result of evaluating the LHS, discover that it doesn’t match my expectations and research, just as the OP did. ![]()
It looks like others have done a nice job pointing Takanori to floating point. (It’s not really a Scala thing. It’s a software engineering thing from about 70 years ago that got squashed into a standard about 40 years ago in IEEE-754. It was a huge achievement at the time.) Stick with floating point to take advantage of the giant community that’s grown up around it and taken it for granted.
When you really care about exactness then floating point is the wrong answer. Much of the time we’ll reach for integer types like Int, and Long (maybe even Short and Byte when we care about storage space). Fractions and division makes that not so nice.
For problems like 0.1 * 0.1 rational numbers (instead of floating point approximations) are a better choice. Spire has a really solid rational number representation encoded for Scala already, so you don’t have to write it yourself. See Spire .
That’s likely overkill for your first day with floating point, but is a good thing to know about when you need to calculate anything with money, especially interest for a big bank. It’s also a somewhat popular job interview question.