Right, so you need an Ordering that depends on your measure function.
Isn’t the ordering fixed at compile time? How can it depend on a function which is chosen at runtime and is different potentially every time takeNsmallest is called?
for{ center <- points
smallOnes = points.sortWith{ (a,b ) => euclidianDistance(a, center) < euclidianDistance(b, center)}.tail.take(N)
} doSomethingWith(smallOnes)
I think you probably are looking for implicit def.
Same as with an explicit function parameter. In the end, the implicit Ordering is just another parameter that just happens to be filled in by the compiler if the context allows for it.
val s: Seq[Int] = Seq(3, 5, 2, 1, 4)
// use global implicit
println(s.sorted)
// explicitly pass ordering as argument
println(s.sorted(implicitly[Ordering[Int]].reverse))
{
// override implicit ordering in scope
implicit val ord: Ordering[Int] = Ordering.by(_.toBinaryString)
println(s.sorted)
}
Ordering[T] type-checks at compile-time but is computed at runtime using the provided implicit Ordring.
Example:
sortedEntries = account.blockedSenders.asScala.toList.sorted(Ordering.by{ (e: EmailBlockedSenders) => e.address.toLowerCase()})
Hope this helps.
I’ve wondered about effective ways to explain implicit values. How to give a conceptual meaning to the logic of “type checks”? I’m curious if this is accurate:
- Implicit values are evidence a value of that type exists. These only type check if the compiler find this evidence in scope.
Funny story…, when I changed this implementation in my code (as a result of this thread) I introduced a funny bug which took me a few days to notice. My original implementation data.sortWith(measure).take(10) returns the list of the 10 smallest elements in sorted order so that the smallest one is at the head. In particular if any element has zero distance, then it is necessarily at the head of the returned list.
When I changed the algorithm, the list returned was still the 10 smallest, but no longer in sorted order, and worse, might have zero distance elements at places other than the head. So I eventually got a division by zero issue, which wasn’t an exception, just resulted in NaN in some weird places in the resulting data, far from the source of the error.
OK, but your functions, benchFold, benchIter, benchNSmallest and benchPlainSort don’t have such a parameter. There’s still something I’m missing.
While it’s accurate I’ve found new learners don’t grok the explanation from that direction. I usually explain that implicits are “helpers” of some sort that the compiler fills in for you when you ask for them. You have to state which helper you want by placing a distinguished value (or a value generator) of the given type in implicit scope. If the compiler cannot find an implicit of the given type then it was never put (or generated) into implicit scope. Contrariwise if the compiler doesn’t complain then your helper was found.
There’s something about showing them implicit val myFoo = Foo(xyz) and then talking about evidence. When I’ve asked the folks I’ve taught they don’t think this is an interesting connection because of course it exists, they just put it there. It’s when you get into implicit defs that generate some complex implicit where speaking about “evidence” clicks.
YMMV of course. ![]()
The bench.* functions don’t - they already bind the concrete type (Int) and just rely on the default implicit Ordering for this type. The .*MinSet functions do, though: They declare a context bound [T : Ordering] (see lang spec §7.4), which basically is sugar for an additional parameter list (implicit xyz: Ordering[T]), where xyz is a compiler-generated identifier.
I cannot really comment on the theoretical foundations, but this feels too condensed - in particular it seems to be missing the distinction between implicit definition (declaration) and implicit parameter (usage). Perhaps better: “Implicit definitions provide evidence that a value of a type exists. (EDIT: Application of methods with) Implicit parameters only type-checks if the compiler finds evidence for the corresponding type in scope.”…?
Implicit values are evidence a value of that type exists. These only type check if the compiler find this evidence in scope.
I would not agree. Consider:
def m(x: A)(implicit y: A): Unit = ???
val a = new A
m(a)
When we looked at the first argument list, we clearly saw that an instance of type A exists, so why would we still need evidence for the existence of such an instance when we look at the second argument list?
It is not about the existence of an instance of A at all, but rather the existence of a special instance we marked as implicit.
You can, of course, replace all statements of the form “x has been defined” with “evidence has been defined, that x exists”, but I’m not sure what this is adding.
And would we soon state that evidence exists that evidence exists that evidence exists?
You could phrase this as evidence supporting the evidence narrative: The compiler requires evidence that an applicable argument value for a parameter exists - either direct evidence through a parameter binding explicitly provided by the caller or, lacking that, derived evidence from an implicit definition. The latter option is only available for parameters explicitly declared implicit. ![]()
So if I am trying to find the 10 smallest elements of a List[(Location,Double)], does that mean I need to provide some implicit value a the point where I call takeNsmallest? And if I want minSet to compare two objects by comparing their Location with (loc1,loc2) => euclidianDistance(loc1,center) - euclidianDistance(loc2,center), then which value of which type do I need to declare?
You need to provide an Ordering[(Location, Double)]. Whether this happens as an explicit argument to #takeNSmallest() or via an implicit definition somewhere in scope of the invocation is up to you. (This could either be a full custom definition of Ordering[(Location, Double)], or you could define an implicit Ordering[Location], relying on existing global implicit Orderings for Double and (A, B) to combine to an Ordering[(Location, Double)].)
An Ordering[Location].
Example: Explicitly passing the Ordering as an argument using SAM notation.
minSet(locs, 2)((a, b) =>
(euclidianDistance(a, center) - euclidianDistance(b, center)).sign.toInt)
I appreciate your attempt to help me understand this point which is apparently clear to everyone but me. I’m not sure whether I should just let the subject politely drop, or whether I should keep pushing until I understand. Especially, since I’ve already solved the original problem sufficiently for my application with the code shown below. On the other hand, it is an issue that has bothered me from the first time I read the explanation in the stair-step book 2 years ago.
What I don’t understand about the example is that I have a List[(Location,Double)] in the scope where takeNsmallest is called, not in the place where takeNsmallest is defined. The call-site is the place where I want to specify how minSet should compare two Locations.
takeNsmallest does not know about center, so the body of the distance function cannot be included in the call of minSet as you suggest. Furthermore, in general I would like to call takeNsmallest using many unrelated types of objects, and the comparison functions themselves, might need to call takeNsmallest.
case class MaxSizeList[T](maxSize: Int, measure: T => Double, givenItems: List[T]) {
def narrowToSize(size: Int, currentItems: List[T]): List[T] = {
if (size > maxSize) { // if the List is too big, the remove the maximum element (once) and try again
val maxElem = currentItems.reduce { (a: T, b: T) => if (measure(a) < measure(b)) b else a }
val maxVal = measure(maxElem)
val (left, right) = currentItems.span(a => measure(a) < maxVal)
narrowToSize(size - 1, left ::: (right.tail))
} else
currentItems
}
val items: List[T] = narrowToSize(givenItems.length, givenItems)
}
def takeNsmallest[T](n: Int, data: List[T], measure: T => Double): List[T] = {
if (n == 0 || data.isEmpty)
List()
else {
data
.foldLeft(MaxSizeList[T](n, measure, List[T]())) { (acc, next) => MaxSizeList(n, measure, next :: acc.items) }
.items
}.sortBy{measure}
}
If it helps your understanding, these two methods are equivalent.
def sort1[T](xs: List[T], measure: T => Double) = xs.sortBy(measure)
def sort2[T](xs: List[T], measure: T => Double) = xs.sorted(Ordering.by(measure))
scala> sort1(List(-3.0, 2.0, 3.0, 5.0 , 6.0), (x: Double) => math.abs(x - 3))
res38: List[Double] = List(3.0, 2.0, 5.0, 6.0, -3.0)
scala> sort2(List(-3.0, 2.0, 3.0, 5.0 , 6.0), (x: Double) => math.abs(x - 3))
res39: List[Double] = List(3.0, 2.0, 5.0, 6.0, -3.0)
In sort2 you pass a custom Ordering to sorted.
Thanks for clarifying that. I think I understand this part. It works because sorted has an optional argument where you can pass the ordering. However, in sangamon’s implementation of the code, the takeNsmallest function DOES NOT have such an argument. Rather it expects the ordering to already be somehow encoded into the type whose instances comprise the list.
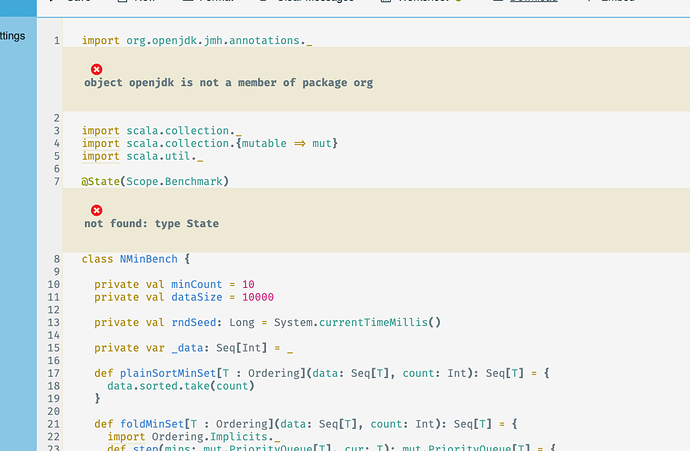
Hi Patrik, When I try to look at yoursample code on Scastie, I get a bunch of errors which i don’t understand.
In the example, the ordering is specified as an explicit argument to #minSet(). I wouldn’t know how to get any closer to the call site. ![]()
Furthermore, in this thread, #minSet() and #takeNSmallest() are functionally equivalent implementations of the same concept, so I don’t really get why they both appear in your question…?
Anyway, for the sake of simplicity, let’s forget about those and focus on Seq#sorted… The signature is:
def sorted[B >: A](implicit ord: Ordering[B]): C
…so it takes an Ordering[B] as an argument. This could equivalently be expressed as
def sorted[B >: A : Ordering]: C
Now let’s create a Location type:
case class Location(x: Double, y: Double)
object Location {
def euclidianDistance(a: Location, b: Location): Double = {
import math._
sqrt(pow(b.x - a.x, 2) + pow(b.y - a.y, 2))
}
def orderingByDist(center: Location): Ordering[Location] =
(a, b) =>
(euclidianDistance(a, center) - euclidianDistance(b, center))
.sign.toInt
implicit val locationDefaultOrdering: Ordering[Location] =
orderingByDist(Location(0, 0))
}
val locs =
Seq(
Location(1, 2),
Location(1, 0),
Location(0, 2),
Location(0, 0),
Location(-1, -2)
)
Now we have a default Ordering[Location] that can be used by Seq#sorted.
println(locs.sorted)
// List(Location(0.0,0.0), Location(1.0,0.0), Location(0.0,2.0), Location(1.0,2.0), Location(-1.0,-2.0))
To sort relative to a different “center”, explicitly pass a custom ordering at the call site:
println(locs.sorted(Location.orderingByDist(Location(1, 0))))
// List(Location(1.0,0.0), Location(0.0,0.0), Location(1.0,2.0), Location(0.0,2.0), Location(-1.0,-2.0))
…or provide an accordingly scoped implicit ordering (“closer” to the call site than the default implicit in the Location companion object):
{
implicit val locationCustomOrdering: Ordering[Location] =
Location.orderingByDist(Location(1, 0))
println(locs.sorted)
// List(Location(1.0,0.0), Location(0.0,0.0), Location(1.0,2.0), Location(0.0,2.0), Location(-1.0,-2.0))
}